23.体積弾性率(断熱操作の場合)（難易度：⭐️）

1. 体積弾性率
2. 理想気体の体積弾性率（断熱操作）

みなさん、勉強おつかれさまです！！

前回の単元では、「体積弾性率」と「等温操作の時の体積弾性率」

について勉強しました。

今回は、この体積弾性率というもの

をいうものを学んでいきましょう！！

1.体積弾性率

まずは、体積弾性率についての復習です！！

はい！体積弾性率というものは、

「大きいほど変形しづらく、小さいほど変形しやすい」です。

この単元では、\(\kappa =-V \frac{dp}{dV}\)の式の \(p\) に

式を代入して計算してみたいと思います！！

2.理想気体の体積弾性率（断熱操作）

前回は、「等温操作のときの体積弾性率」を計算しました。

今回は、「断熱操作」です！！

断熱操作というのは、イメージ的には、

「熱の出入りが全くないようにした環境」

イメージ的には、外の世界とのやりとりをシャッタアウトした世界です。

そして、いま考えている状態、つまり

「断熱操作での理想気体」を考えるとき

ある法則を使うことができます。。

それはなにかというと、「ポワソンの法則」です。

この式も今回の計算で使っていきますので、

押さえておきましょう！！

わからなくなったら、いつでも戻ってきましょうね！！

ここでひと段落つきましょうか、、

よく体力を回復してから次の単元に行きましょう！！笑

導出

それでは、実際に計算していきましょう。

まず、ポワソンの法則を変形します。

を、体積弾性率\( \gamma\)の定義

$$\kappa =-V \frac{dp}{dV}$$

に代入して計算して行きます。ここからは

単純な計算なので自分で式を追ってみましょう。

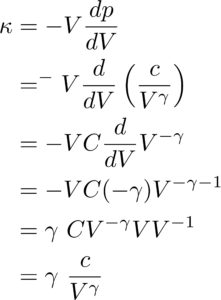
さて、ここまで計算することができたでしょうか？

そして、最後の締めにあることをします！

ここで、ポワソンの法則を思い出してみます！

これを使うと、最後の結果を少し変形できることに

気がつくでしょうか、、

はい！整理すると、

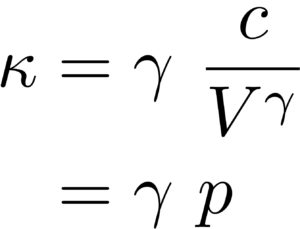
つまり、断熱操作の場合

「体積弾性率＝\( \gamma \times 圧力\)」

となるのです！！

となります！！

この単元は以上です！お疲れ様でした！