目次
みなさん、勉強おつかれさまです!!
前回の単元では、「理想気体がする仕事」について
1.理想気体がする仕事
毎度恒例、前回の復習です!!
「理想気体のする仕事」は
体積が、\(V_1\)から、\(V_2\)へ体積が増えたとすると、
![]()
という風にかくことができました。
ここで納得できなかったら、
遠慮なく前の単元にもどってくださいね!
地道にやることがいちばんの近道です!!
よくみると、この式の中に「積分」が入っていますね?
この単元では、もっと想像しやすい状況を考えて
この積分を実行することで、「理想気体のする仕事」を
2.理想気体がする仕事(等温変化)
さて、先ほどの理想気体のする仕事をかいたときに、
体積が、\(V_1\)から、\(V_2\)へ体積が増えたとする と言いました。
この変化が、「等温変化」の場合を考えます。
熱平衡状態の記述の方法で表すと、
状態が\((T;V_1,N)\)から、\((T;V_2,N)\)に変化するので、
$$(T;V_1,N)\overset{}{\longrightarrow}(T;V_2,N)$$
と書きます。
特に、「等温操作」であるので、
$$(T;V_1,N)\overset{i}{\longrightarrow}(T;V_2,N)$$
という状況です。
このときにした仕事を求めてみましょう。
計算するときに注意することは、今回は温度:\(T\)が一定になるということです。
つまり、インテグラルのあとの\(T\)をそとに出すことができます!!
いいですか?! いつでも温度\(T\)が一定なわけではなく、
「等温変化なので、温度\(T\)は一定」なのです。
これを用いて積分をしてみると、
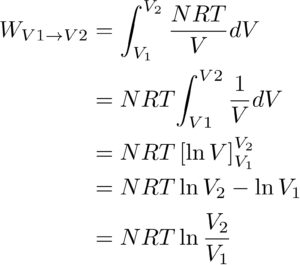
という風に積分をすることができて、
とても簡単な式にすることができました!!
理想気体がする仕事(等温変化)
「理想気体のする仕事:\(W\)」は
体積が、\(V_1\)から、\(V_2\)へ体積が増えたとすると、
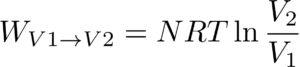
となる。
はい!
結果的に、複雑だった「理想気体のする仕事」が
簡単な式で表すことができました!!
まとめ
- 理想気体がする仕事
![]()
- 理想気体がする仕事(等温変化)
![]()
この単元は以上です!お疲れ様でした!



コメントを残す