目次
みなさん、勉強おつかれさまです!!
前回の単元では、「等温変化で理想気体がする仕事」について
1.理想気体がする仕事
さて、今回もまずは復習です!!
いままで、何回も出てきましたが、
「理想気体のする仕事」は
体積が、\(V_1\)から、\(V_2\)へ体積が増えたとすると、
![]()
という風にかくことができました。
今日もこの式を存分に使います!!
この式が自分の手足のようにつかう準備を
していてくださいね!!
前回の単元では「等温変化」の場合を考えました。
2.理想気体がする仕事(断熱変化)
まずは「断熱変化」という言葉についておさらいです!!
「断熱変化」というのは、
「熱の出入りが全くないようにした環境」
イメージ的には、外の世界とのやりとりをシャッタアウトした世界です。
さて、先ほどの「理想気体のする仕事」の式をかいたときに、
体積が、\(V_1\)から、\(V_2\)へ体積が増えたとする と言いました。
この変化が、「断熱変化」の場合を考えます。
ちなみに、断熱変化を熱平衡状態の記述の方法で表すと、
状態が\((T;V,N)\)から、\((T’;V’,N’)\)に変化する時、
$$(T;V,N)\overset{}{\longrightarrow}(T’;V’,N’)$$
と書きます。
特に、「断熱操作」であることを強調したい場合は、
この矢印の上に「\(a\)」を書くことで、
$$(T;V,N)\overset{a}{\longrightarrow}(T’;V’,N’)$$
と表します。
このときにした仕事を求めてみましょう。
そして、今回つかう重要事項がもうひとつあります!
それは「ポワソンの法則」というものです。
ポワソンの法則
理想気体の断熱変化
$$(T;V,N)\overset{a}{\longrightarrow}(T’;V’,N’)$$
では、以下の式が成り立つ。
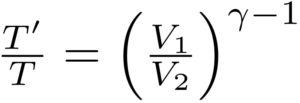
\( \gamma=\frac{C_p}{C_v}\)
今回は、この式も用いて、積分を計算していきます。
積分をするまえに、まず、\( \frac{T’}{T}\)を2通りの方法で計算します。
1通り目
いま考えているのは、理想気体です。
理想気体というのはボイル・シャルルの法則
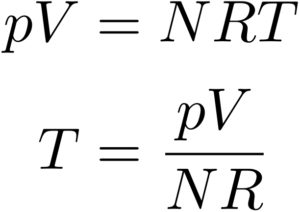
が成り立つので、これを用いると、
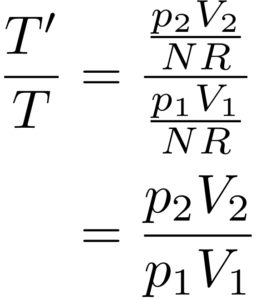
という風に計算することができました!
2通り目
ここで、先ほど紹介した「ポワソンの法則」を使います。
「ポワソンの法則」より、
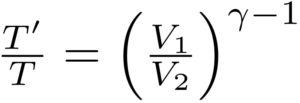
となります。
以上より、\( \frac{T’}{T}\)を二つの式で表すことができました。
なので、これらの二つを=で結んでみると、、
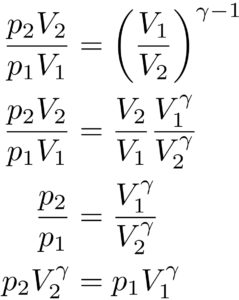
という風に変形することができました。
この式を用いると、二つのある状態の圧力と体積の関係がわかることになります。
つまり、
「圧力\(p_1\),体積\(V_1\)」
「圧力\(p\),体積\(V\)」
という二つの状態において、
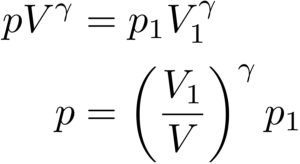
という関係式を導くことができます。
同じようにして、
「圧力\(p_1\),体積\(V_1\)」
「圧力\(p_2\),体積\(V_2\)」
という二つの状態において、
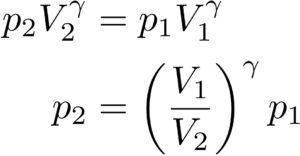
という関係式を導くことができます。
はい!!これで準備は整いました!!
早速積分をしていきたいと思います!!
スタートの式は、毎度恒例
![]()
です!!
まず、この式に、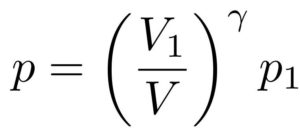
を代入して計算していくと、
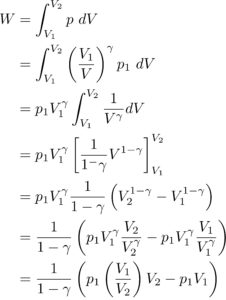
次に、![]()
を用いることで、さらに変形することができて、
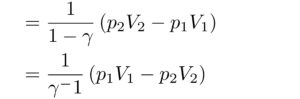
はい!これがまさに
「断熱変化で理想気体がする仕事」です!!
理想気体がする仕事(断熱変化)
「断熱変化で、
理想気体のする仕事:\(W\)」は
体積が、\(V_1\)から、\(V_2\)へ体積が増えたとすると、
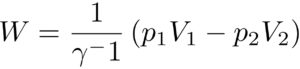
となる。
はい!
結果的に、複雑だった「理想気体のする仕事」が
簡単な式で表すことができました!!
今回は、計算が多くて、大変でしたね。。
ゆっくり休んでくださいね^^
まとめ
- 理想気体がする仕事
![]()
- 理想気体がする仕事(断熱変化)
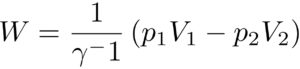
この単元は以上です!お疲れ様でした!



コメントを残す