この記事では、具体的に群の例を見てみましょう。
例1 R\(\backslash\){0}
実数全体の集合から0のみを抜いた集合R\(\backslash\){0}は群になります。群というからには先ほどの3つのルール(G1)~(G3)を満たすことを確かめてみましょう。
証明(厳密な証明ではなく成り立つ具体例をみることにします)
(G1)
たとえば、3つの数をもってきます。では、15と3と6にしましょう。(G1)が言っていることは、\(15\cdot(3 \cdot 6)=(15 \cdot 3) \cdot 6\)が成り立つということです。これは明らかですよね?
(G2)
(G2)が言っていることは、ある数に右からかけても左からかけても数がかわらないような数があるということです!どうでしょうか?思いついた人は天才!!答えは「1」です!1をある数の右からかけても左からかけてもその掛けられた数の値は変化しないですよね?
(G3)
最後に(G3)です!(G3)の言っていることは、Gのどの数に対しても、ある数があって、その数を右からかけても左からかけても結果は1になるという数があると言っています。さて、ちょっとさっきと似てる問題です!どうでしょうか…..試しに、4の逆元を考えてみましょう。4にかけて1になる数はなにがあるでしょうか…..はい!\(\frac{1}{4}\)です!このように考えると、ある数があってその逆数の数を考えることですべての数に逆元があることになります!
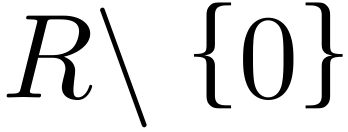
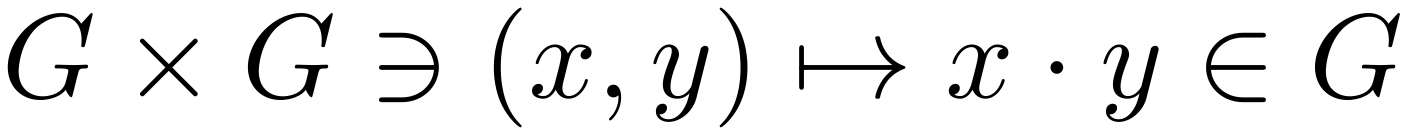

コメントを残す