集合Gに演算(・) が定義されていて、
$$ G \times G \ni (x,y) \mapsto x \cdot y \in G $$
が定義されていて、演算(・)が次の三つの規則を満たすときGを群といいます。
(G1)(結合法則)
G内のすべての元、\(x,y,z\)に対して、$$(x\cdot y)\cdot z=x \cdot(y\cdot z)$$が成り立つ。
(G2)(単位元の存在)
単位元という元\(e \in G\)がGの中にあって、Gのどの元\(x\in G\)に対しても、$$e\cdot x=x \cdot e=x$$が成り立つ。
(G3)(逆元の存在)
Gのどの元\(x\in G\)に対しても、逆元という元 \(x^{-1}\in G\)がGの中にあって、$$x^{-1}\cdot x= x \cdot x^{-1}=e$$が成り立つ。
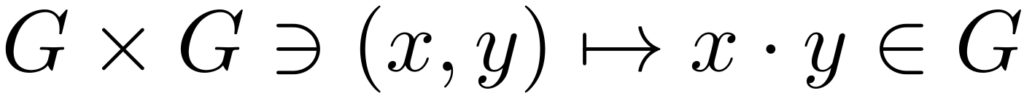

コメントを残す